Balancing Act

The past few days I have been learning the basics of some useful telecommunications principles. I started with a search for a line code that would eliminate long runs of 0s and 1s in the pulses recorded to tape. The tests from the previous log show how long runs of like-pulses cause a DC drift. After some reading I learned about disparity and DC-balanced codes that exist to please channels where a DC component is problematic. I decided to look for a code that would satisfy both requirements of being run length limited and DC balanced.

First I came across 8b10b. The efficiency of the coding looked promising (10bits to represent an octet), but the complexity of implementation was a bit of a turnoff. Each code-word is unbalanced, meaning running DC imbalance has to be calculated and countered during the encoding process. This combined with the need to craft a large word table means 8b10b would be tricky to implement correctly and may not work as well as a code that has DC balanced code words.

After more searching I came across something much simpler that satisfied both requirements: The line code from Slice TS-FO-02 of IEEE 1355. This line code is intended to be used in optical cable at a rate of 200 megabits/sec. A stream on input octets (called data characters in Wiki’s spec summary) are split into 2 4-bit symbols (bits 0..3 in the first, 4..7 in the second) that are each mapped to a DC-balanced 6-bit word. The code is DC balanced and limited to a run of 4 like bits using the table provided by the specification summary. Because there are more 6 bit words than 4 bit symbols, there are reserved words that are used in link control sequences. Below is a table of the code word mapping from the specification modified to explicitly assign fixed control characters. Words in the right column are transmitted leftmost bit first.

Data	Balanced Word
0	011010
1	101001
2	011001
3	110001
4	001101
5	101100
6	011100
7	110100
8	001011
9	100011
A	010011
B	110010
C	001110
D	100110
E	010110
F	100101
CTRL1	101010
CTRL2	010101

It is possible to construct bit sequences that cannot exist in or across the boundaries of encoded data words using combinations of control words. These combinations can be used as syncwords to frame segments of data in a bit-stream. I would like to explore frame synchronization as a mechanism for minimizing data loss due to corruption of part of the payload and as a way to enable seeking though data streams using the tape transport. The use of unique syncwords would also enable detection and correction of phase-reversal that can be caused by different record and playback hardware.

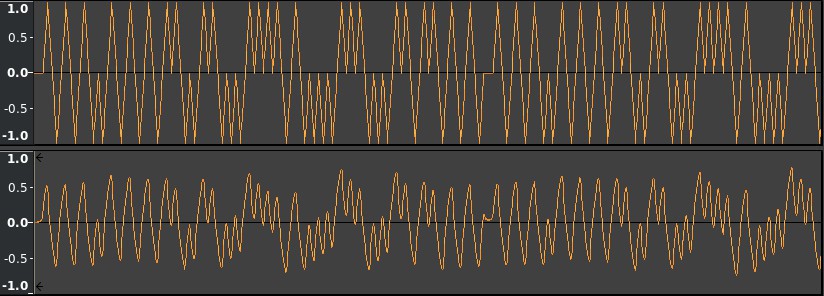
I tested this code out by recording and playing a long run 6-bit words at 2400 bits/sec. I chose this speed because it appears to be near the minimum stable speed my tape deck will reproduce without serious DC drift of runs of like bits. The test bit stream was assembled to include the longest runs of like bits possible using the table above. The test stream was CTRL 1, CTRL 2, 9, 7, C, 4, CTRL1 (101010010101011001100011110100001110001101101010):

The recovered waveform drifted a small amount in repeated runs of bits, but does not drift very far. The silent spot in the middle of the above screenshot is a gap between repeated bit patterns in the WAV file generated by my script. I included the spaces as a visual marker in the wave pattern; they will not be included in future tests. I could not get my USB sound card to play a very short bit pattern so I repeated it several times and recorded the longer pattern. In the test the bit pattern was repeated 8 times, but the playback only captured 2 (exactly 2) repetitions of the bit pattern. I’m not sure what caused this, but more experimentation is needed with other audio hardware and software to pinpoint what is to blame. Now that I have a line code to experiment with I can start working on the C code that encodes and decodes raw bit streams from audio streams.